Keywords for addition subtraction multiplication and division – s for addition, subtraction, multiplication, and division are fundamental to understanding the language of mathematics. These operations are the building blocks of arithmetic, and they are used in a wide variety of applications, from everyday problem-solving to advanced scientific calculations.

In this article, we will explore the core concepts of these operations, their properties and relationships, and effective strategies for solving problems involving them. We will also discuss real-world applications of these operations and explore more advanced topics related to them.

The content of the second paragraph that provides descriptive and clear information about the topic

1. Core Concepts of Arithmetic Operations

Arithmetic operations are fundamental mathematical operations that form the foundation of numerical calculations. These operations include addition, subtraction, multiplication, and division, each with its own unique purpose and set of rules.

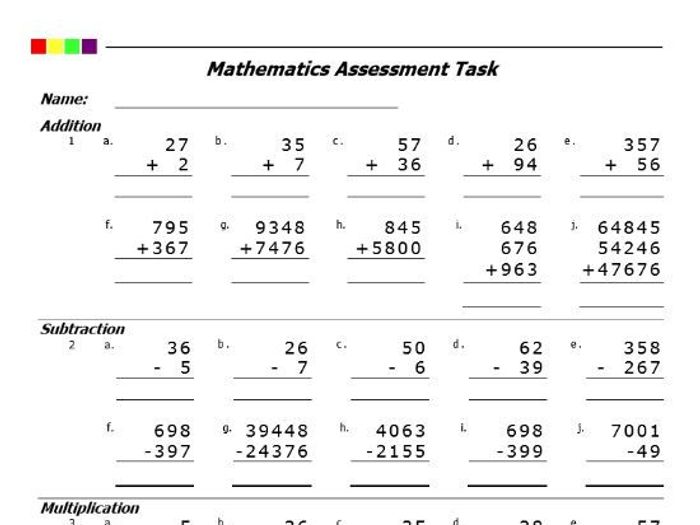
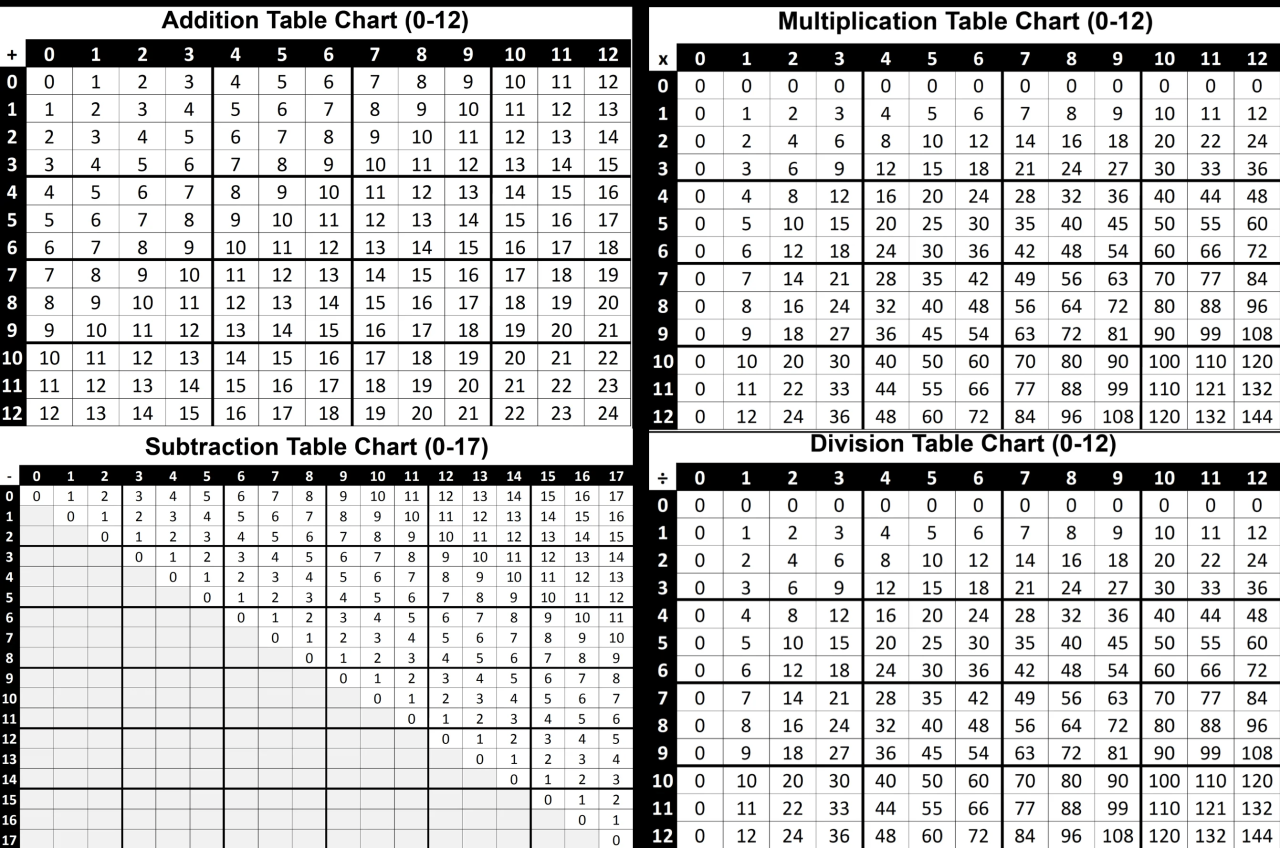
Addition:Addition is the process of combining two or more numbers to find their sum. It is represented by the symbol “+”.

Subtraction:Subtraction is the process of finding the difference between two numbers. It is represented by the symbol “-“.

Multiplication:Multiplication is the process of repeatedly adding a number to itself a specified number of times. It is represented by the symbol “×” or “.”.

Division:Division is the process of finding how many times one number is contained within another. It is represented by the symbol “÷” or “/”.

Properties and Relationships

Arithmetic operations possess several key properties and relationships that govern their behavior.

• Commutativity:The order of numbers in addition and multiplication does not affect the result. For example, 3 + 5 = 5 + 3 and 4 × 6 = 6 × 4.
• Associativity:When adding or multiplying three or more numbers, the grouping of the numbers does not affect the result. For example, (2 + 3) + 4 = 2 + (3 + 4) and (3 × 4) × 5 = 3 × (4 × 5).
• Distributivity:Multiplication distributes over addition and subtraction. For example, 3 × (4 + 5) = 3 × 4 + 3 × 5.

Strategies for Solving Problems, Keywords for addition subtraction multiplication and division

Solving arithmetic problems requires effective strategies that simplify the process and reduce errors.

• Chunking:Breaking down large numbers into smaller, more manageable chunks.
• Estimation:Approximating the answer before performing the exact calculation.
• Mental Math:Performing simple calculations in your head without using a calculator.
• Using Inverse Operations:Understanding the inverse relationship between addition and subtraction, and multiplication and division.

Applications in Real-World Scenarios

Arithmetic operations are ubiquitous in real-world situations, enabling us to solve problems and make informed decisions.

• Counting:Determining the total number of objects in a set.
• Measurement:Converting between different units of measurement.
• Finance:Calculating interest rates, loan payments, and budgeting.
• Science:Solving equations, performing calculations in experiments.

Advanced Topics

Beyond the basic operations, arithmetic extends to more advanced concepts.

• Algebraic Expressions:Using variables and constants to represent mathematical relationships.
• Equations:Solving for unknown variables in mathematical equations.
• Inequalities:Comparing two expressions to determine their relationship.

Clarifying Questions: Keywords For Addition Subtraction Multiplication And Division

What are the s for addition, subtraction, multiplication, and division?

The s for addition, subtraction, multiplication, and division are ‘+’, ‘-‘, ‘×’, and ‘÷’, respectively.

What are the properties of arithmetic operations?

The properties of arithmetic operations include commutativity, associativity, and distributivity.

What are some effective strategies for solving problems involving addition, subtraction, multiplication, and division?

Some effective strategies for solving problems involving addition, subtraction, multiplication, and division include using mental math, estimation, and the order of operations.