Which statement is true about the residual plot below? The residual plot is a graphical representation of the residuals, which are the differences between the observed values and the predicted values from a regression model. By examining the residual plot, we can assess the model’s fit and identify potential issues with the model’s assumptions.
The x-axis of the residual plot represents the predicted values, while the y-axis represents the residuals. The horizontal line at zero on the y-axis represents the line of perfect fit, where the observed values are equal to the predicted values.
The distribution of the residuals around the horizontal line indicates the model’s fit. If the residuals are randomly scattered around the line of perfect fit, it suggests that the model is a good fit for the data.
Identifying the Purpose of the Residual Plot
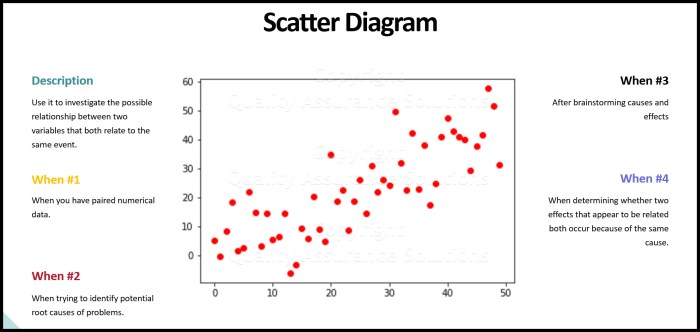
In regression analysis, a residual plot is a graphical representation of the residuals, which are the differences between the observed values of the dependent variable and the predicted values generated by the regression model. Examining the residual plot serves several important purposes:
- To assess the overall fit of the regression model and identify any potential issues.
- To evaluate whether the assumptions of the regression model are met.
- To detect outliers or influential points that may affect the model’s predictions.
Understanding the Components of the Residual Plot: Which Statement Is True About The Residual Plot Below
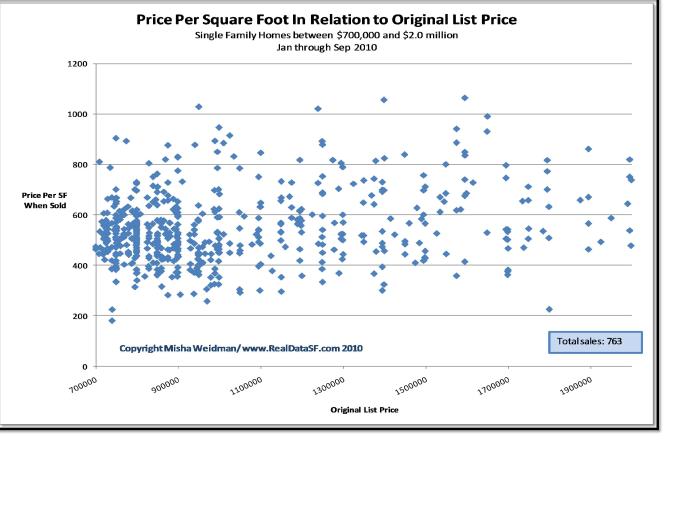
The residual plot typically consists of the following components:
- X-axis:The x-axis represents the independent variables or the predicted values.
- Y-axis:The y-axis represents the residuals, which are the differences between the observed and predicted values.
- Horizontal line at zero:This line represents the perfect fit, where all the residuals are zero and the model’s predictions perfectly match the observed values.
- Distribution of residuals:The distribution of the residuals around the horizontal line provides insights into the model’s fit and the assumptions it makes.
Interpreting the Residual Plot
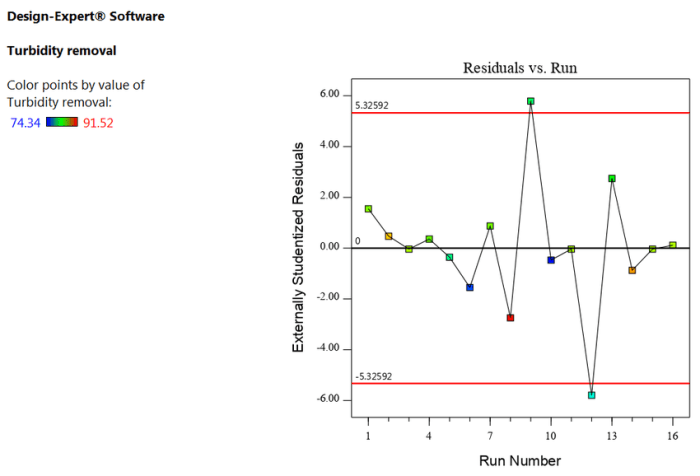
Patterns in the residual plot can indicate potential issues with the regression model. Some common patterns to look for include:
- Non-random patterns:If the residuals show a non-random pattern, such as a curve or a trend, it may indicate that the model is not capturing the relationship between the variables adequately.
- Large spread of residuals:A large spread of residuals indicates that the model is not predicting the dependent variable accurately.
- Outliers or influential points:Outliers are residuals that are significantly different from the rest of the data. Influential points are data points that have a disproportionate effect on the model’s predictions.
Evaluating Model Assumptions
The residual plot can also be used to evaluate whether the assumptions of the regression model are met. These assumptions include:
- Linearity:The relationship between the independent and dependent variables should be linear.
- Homoscedasticity:The variance of the residuals should be constant across all values of the independent variables.
- Normality:The residuals should be normally distributed.
Violations of these assumptions can affect the validity of the regression model and its predictions.
Clarifying Questions
What is the purpose of a residual plot?
The purpose of a residual plot is to assess the fit of a regression model and identify potential issues with the model’s assumptions.
What does the x-axis of a residual plot represent?
The x-axis of a residual plot represents the predicted values.
What does the y-axis of a residual plot represent?
The y-axis of a residual plot represents the residuals.
What does the horizontal line at zero on the y-axis represent?
The horizontal line at zero on the y-axis represents the line of perfect fit.
What does the distribution of the residuals around the horizontal line indicate?
The distribution of the residuals around the horizontal line indicates the model’s fit.