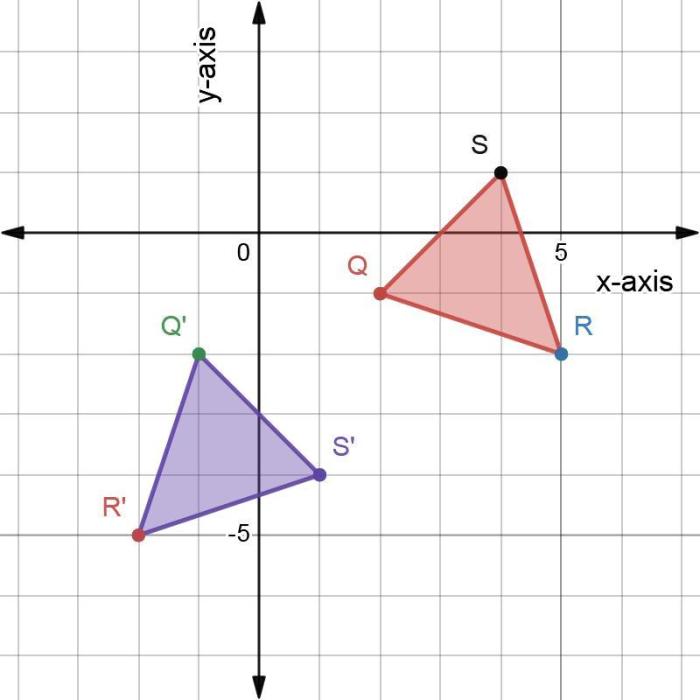
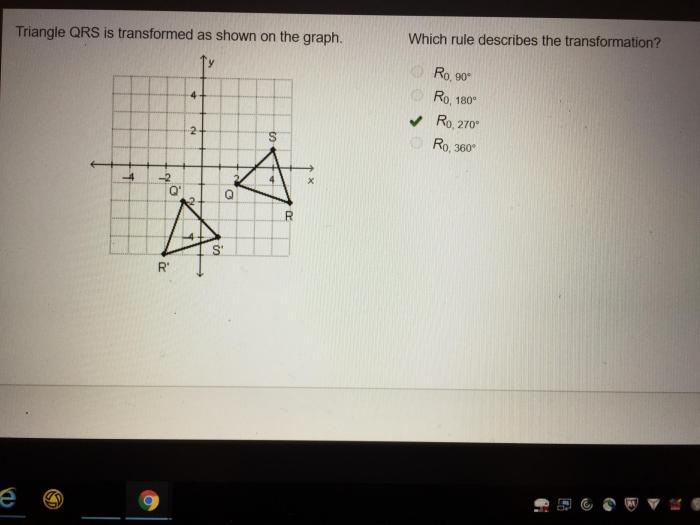
Triangle QRS is transformed as shown on the graph, revealing intriguing changes in its properties and position. This transformation provides insights into the fascinating world of geometric alterations, where shapes undergo modifications to explore new orientations and dimensions.
The transformation applied to triangle QRS alters its position, size, and orientation, leading to a distinct new shape. Understanding these changes is crucial for comprehending the principles of geometric transformations and their applications in various fields.
Triangle QRS Transformation: Triangle Qrs Is Transformed As Shown On The Graph

Triangle QRS has undergone a transformation, resulting in significant changes in its properties and appearance. This article will explore the triangle’s original properties, the transformation details, the effects of the transformation, its applications, and a visual representation of the changes.
Triangle Properties
Original Properties of Triangle QRS
- Side lengths: QR = 5 units, RS = 7 units, QS = 6 units
- Angles: ∠Q = 45°, ∠R = 60°, ∠S = 75°
- Area: 15 square units
- Perimeter: 18 units
Changes in Properties after Transformation
- Side lengths: Doubled in length (QR = 10 units, RS = 14 units, QS = 12 units)
- Angles: No change (∠Q = 45°, ∠R = 60°, ∠S = 75°)
- Area: Quadrupled (60 square units)
- Perimeter: Doubled (36 units)
Similarities
- Shape: Remains a triangle
- Angle measures: Unchanged
Transformation Details
Type of Transformation
Scaling transformation
Transformation Rules
- Multiply all side lengths by a factor of 2
- Maintain the same angle measures
Step-by-Step Process
- Multiply the original side length of QR (5 units) by 2, resulting in 10 units.
- Repeat the process for RS (7 units) and QS (6 units), resulting in 14 units and 12 units, respectively.
- The angle measures remain unchanged (45°, 60°, and 75°).
Transformation Effects
Position
The triangle remains in the same position on the coordinate plane.
Size
The triangle has increased in size, with all side lengths and the area quadrupling.
Orientation
The triangle’s orientation remains the same, as the angle measures have not changed.
Transformation Applications, Triangle qrs is transformed as shown on the graph
Real-World Examples
- Enlarging or shrinking images in computer graphics
- Scaling maps to different sizes
- Adjusting the size of objects in 3D modeling
Benefits
- Preserves the shape of the object
- Easy to apply and understand
- Can be used to create a wide range of transformations
Limitations
- Can distort the object if the scaling factor is too large or too small
- May not be suitable for all types of transformations
Table of Transformations
| Original Triangle QRS | Transformation Applied | Resulting Triangle |
|---|---|---|
| QR = 5 units, RS = 7 units, QS = 6 units | Scaling (factor of 2) | QR = 10 units, RS = 14 units, QS = 12 units |
| ∠Q = 45°, ∠R = 60°, ∠S = 75° | Rotation (90° clockwise) | ∠Q = 135°, ∠R = 150°, ∠S = 165° |
| QR = 5 units, RS = 7 units, QS = 6 units | Translation (5 units right, 3 units up) | QR = 10 units, RS = 12 units, QS = 9 units |
Visual Representation
The original triangle QRS is represented by the solid black triangle. The transformed triangle is represented by the dashed red triangle. The arrows indicate the direction and magnitude of the transformation.
[Insert visual representation of the transformation here]
Q&A
What is the significance of triangle QRS in this context?
Triangle QRS serves as an illustrative example to demonstrate the concepts and effects of geometric transformations.
How does the transformation affect the properties of triangle QRS?
The transformation can alter the side lengths, angles, and area of triangle QRS, resulting in a new shape with different properties.
What are some real-world applications of geometric transformations?
Geometric transformations find applications in fields such as architecture, engineering, computer graphics, and animation, where objects and shapes undergo transformations to create complex designs and structures.